|
|
Before fractal geometry was actually made into a kind of math we
had been realizing that nature behaves differently than geometry wants it to.
Mathematicians drew strange shapes that geometry could not explain. Listed are
some of these shapes and people who studied mathematics that “broke the rules.”
|
 |
Cantor
Dust
This was the first of the monsters. Henry Smith
discovered it in 1875, but Greog Cantor got it named after him. This
was the first of the fractals. This “monster” took a line, cut it
into three, and removed the middle third. Then it repeated on the
two lines left over and the next four and so on. If you zoomed in on
one of the small lines it would have the same branching pattern as
the first.
|
|
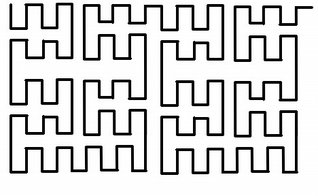 |
The Peano Space
It was discovered in
Giuseppe Peano in 1890. This squiggly line was a counterexample
to the statement: Lines don’t take up space. The Peano Space was
a space-filling curve. It filled every requirement for a curve,
but it did something unusual. It visited every point on a graph,
meaning it took up space.
|
|
 |
Koch Curve/ Snowflake
Helge von Koch discovered this
monster in 1904. This fractal was also a curve. It took a line and put a
triangle in the center. Then on each section it added another triangle,
and then it repeated. This meant that the curve had an infinite measure.
It could be infinitely long and is infinitely precise.
|
|
 |
The Sierpinski Gasket
Vaclav Sierpinski discovered
the Sierpinski Gasket in 1916. It took an equilateral triangle and drew
an upside down triangle in the center. Then on the three smaller
equilateral triangles the step repeated. If you zoomed in on the
triangle it would exactly the same as the first part. A special property
about the Sierpinski Gasket is that it could be made with the Pascal’s
Triangle. If you shaded the odd numbers in on the triangle, the
Sierpinski Gasket’s pattern appears.
|
Each of these “monsters”
set the definition of fractal and got the ball rolling for fractal
geometry. Mathematicians did not approve of these shapes. They were
not smooth like most shapes they were used to. They considered these
shapes just to be drawings, nothing mathematical.
Gaston Julia
He studied the complex plane and
how it works. Julia was interested in what happens when you take a number
and put it into a formula, then take the number you get out and put it back
in again. Julia made many different formulas, but he would never see what
they looked like when graphed.
Poincaré
1884 the King
of Sweden and Norway, Oscar II, asked a Swedish professor to organize a
math competition. The goal was to prove that planets follow cycles. Poincaré
participated in this competition. He proved that three planets will always
follow a cycle, and he won the prize. However he realized that he made a
mistake and that planets may not follow cycles. He then made formulas that
created strange, seemingly unpredictable patterns. This is when "chaos" was
found.

This is an animation of a graph describing chaos.
|
|